Strongly measurable functions
Strong measurability has a number of different meanings, some of which are explained below.
Values in Banach spaces
For a function f with values in a Banach space (or Fréchet space) X, strong measurability usually means Bochner measurability.
However, if the values of f lie in the space 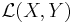 of continuous linear functionals from X to Y, then often strong measurability means that fx is Bochner measurable for each
of continuous linear functionals from X to Y, then often strong measurability means that fx is Bochner measurable for each 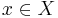 , whereas the Bochner measurability of f is called uniform measurability (cf. "uniformly continuous" vs. "strongly continuous").
, whereas the Bochner measurability of f is called uniform measurability (cf. "uniformly continuous" vs. "strongly continuous").
Semi-groups
It is well known that a semigroup of linear operators is always strongly measurable and strongly continuous but it is uniformly measurable if and only if it is uniformly continuous, i.e., if and only if its generator is bounded.